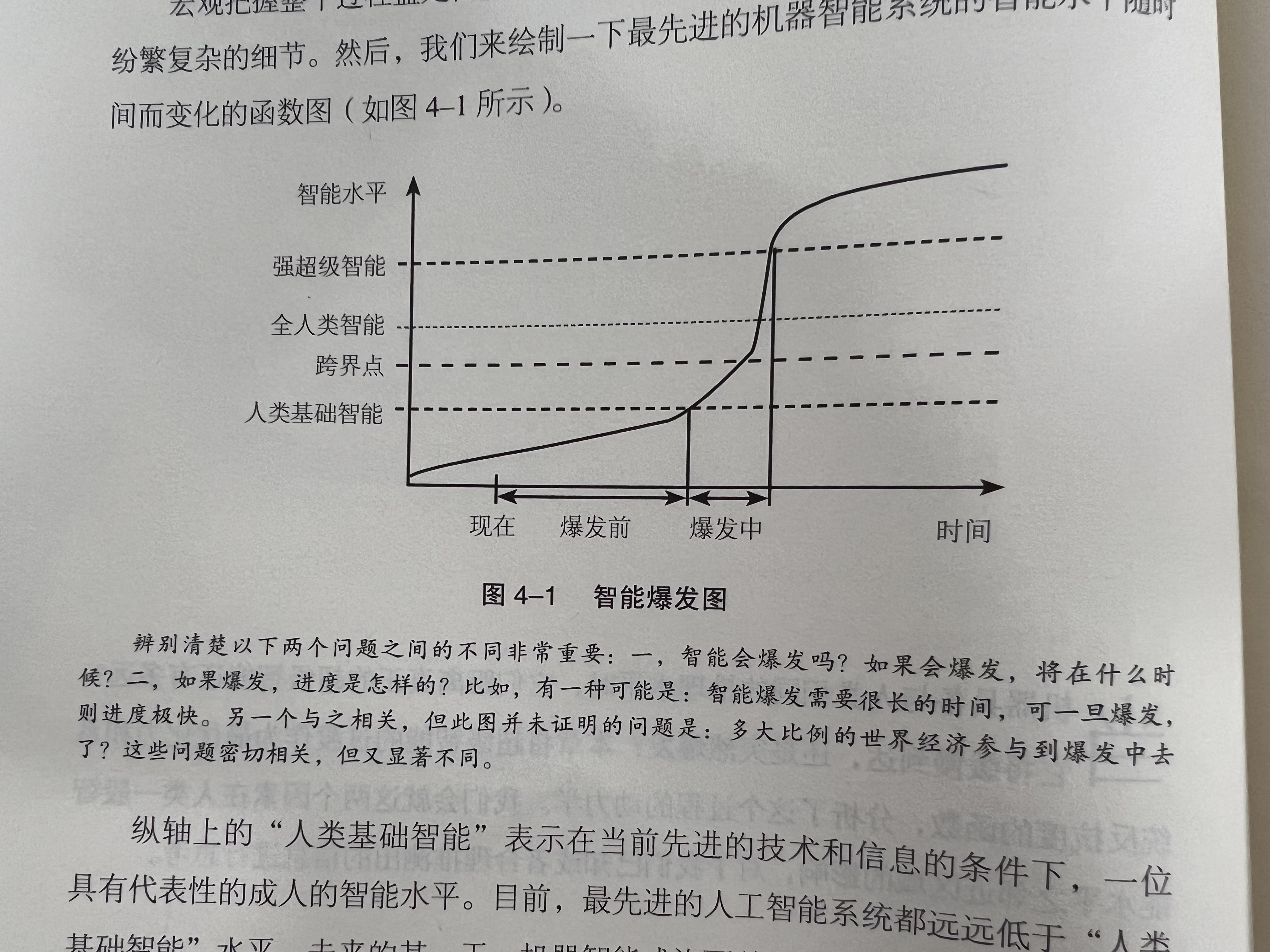
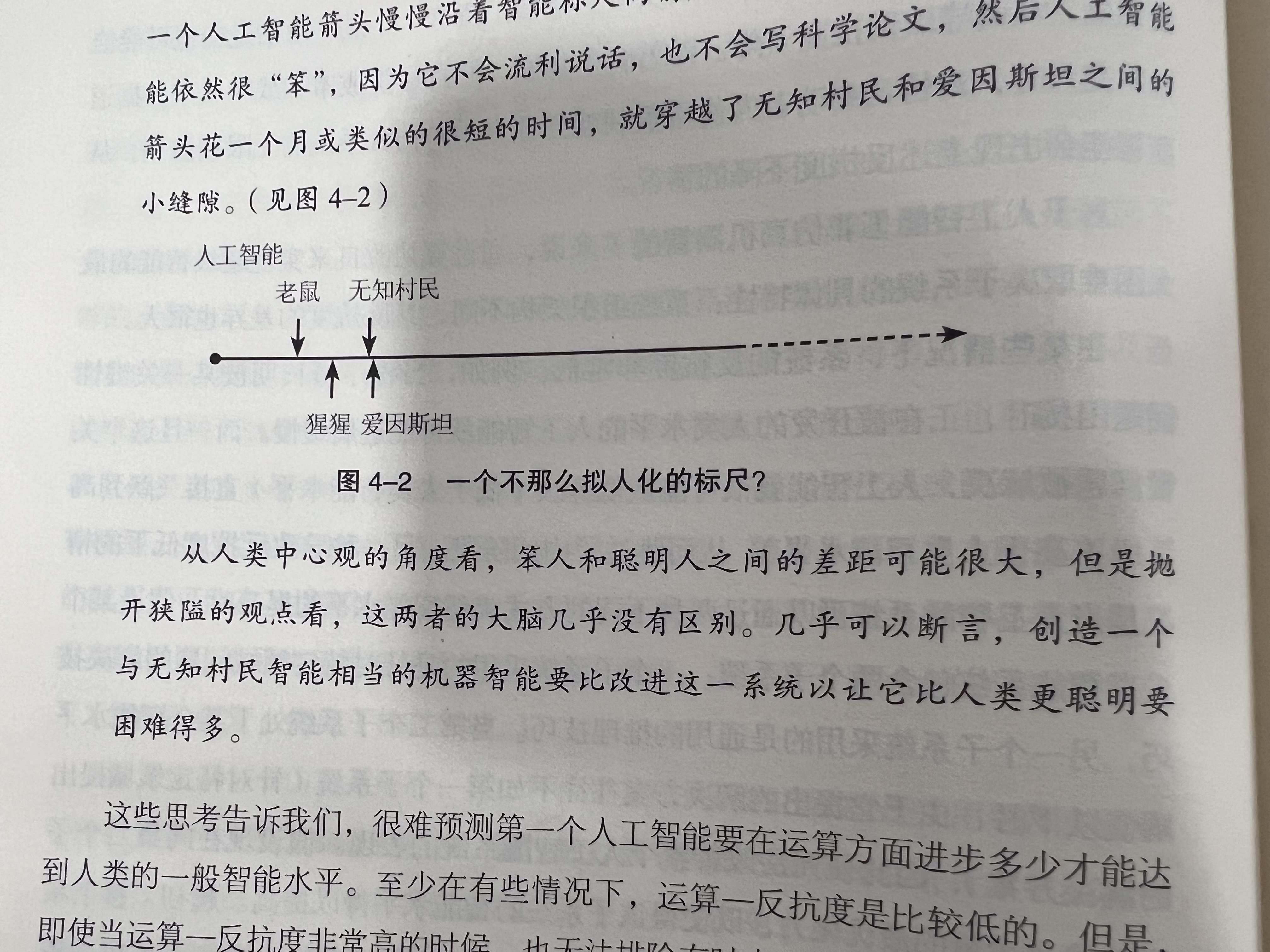
延伸阅读4:

智能大爆发的动力学分析

我们可以把智能变化率写成应用于系统的最优化力与系统的反抗度之间的比率：

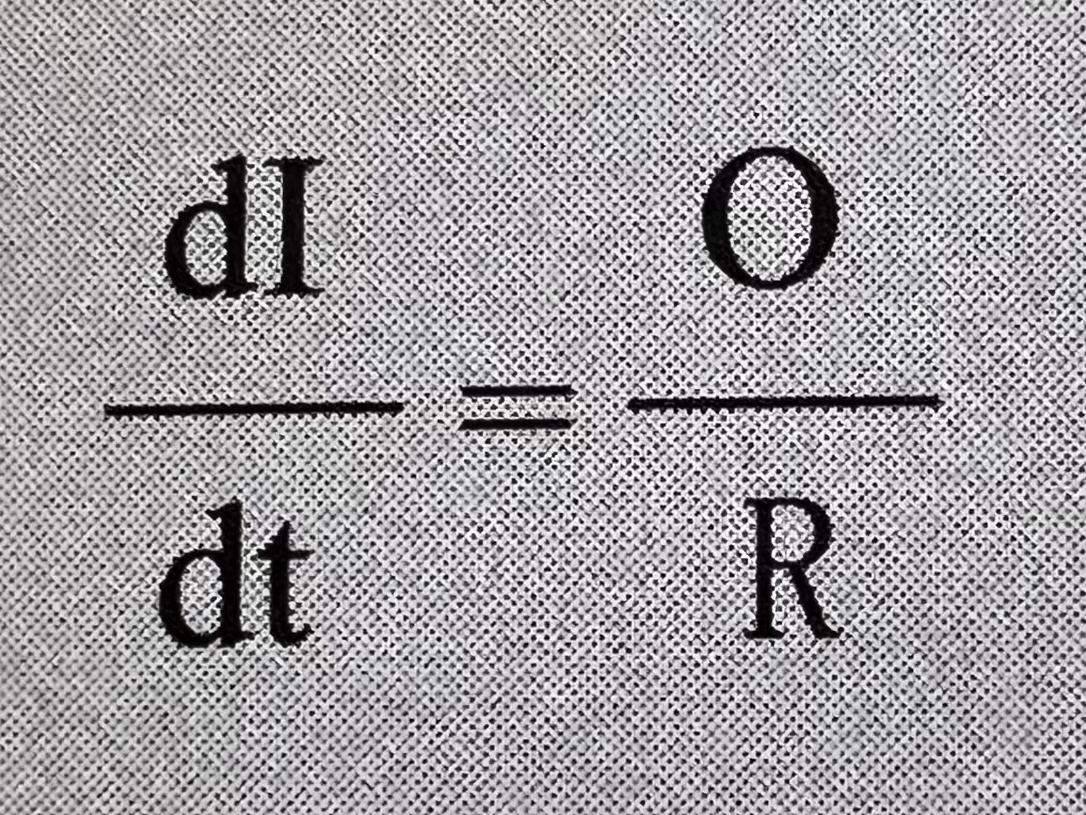
于系统的最优化力的量是系统本身贡献的最优化力以及其他最优化力的总和。例如，一个种子人工智能可能会通过将自身努力和人类项目组的努力结合起来而得到提高，并且可以依靠更广泛的全球研究人员的共同体在半导体工业、计算机科学和相关领域取得的持续进步：

O=O 系 统 +O 工 程 +O 世 界

种子人工智能开始时的认知能力十分有限。因此，一开始O 系 统 很小，而O 工 程 和O 世 界 如何呢？在某些情况下单一项目比世界上其他所有项目有更多的相关能力，例如曼哈顿项目就在洛斯阿拉莫斯国家实验室聚集了世界上最好的物理学家来研制原子弹。更为普遍的是，任何一个项目只包含了世界上相关研究能力的很小一部分。但即便是当外部的世界比一个研究项目有更多相关的研究能力时，O 工 程 仍然可能超过O 世 界 ，因为很多外部世界的能力并没有集中于特定系统中的问题。如果一个项目开始看起来很有前景，也就是当一个系统超过人类基本水平之后而不是之前，它就可能会吸收更多的投资用以增加O 工 程 。如果工程基本是公开的，那么随着其进展就将吸引更多人参与机器智能的工程以及多样化能力的竞争，O 世 界 也可能会上升。因此，在过渡阶段，随着系统能力的增加，应用于改善认知系统的总的最优化力很有可能得到提升。

随着系统能力的增长，可能会到达一个点，即系统本身产生的最优化力开始主导从外部应用于系统的最优化力（穿过所有重要的改进层面）：

O系 统 ＞O工 程 +O世 界

这一跨界点之所以重要，是因为若超越了这一点，进一步提高系统能力会在很大程度上造成应用于改善系统的总体最优化力的增加。我们会因此进入强烈的递归性自我改良系统。这会导致一个相当广范围内的不同形状反抗度曲线下的系统能力的爆发性增长。

为了进一步说明，首先考虑一个反抗度恒定的情景，由此人工智能增长率取决于所应用的最优化力。假定所有应用的最优化力来自人工智能本身，且人工智能将其所有的智能用于扩大其自身智能，也就是O体 系 = I，我们可以得出：

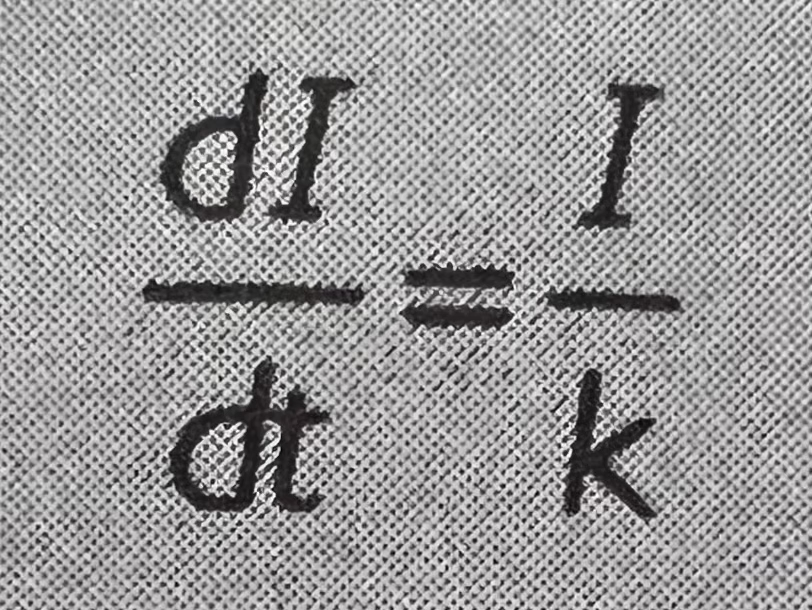
解这个简单的微分方程，从而得出指数函数：

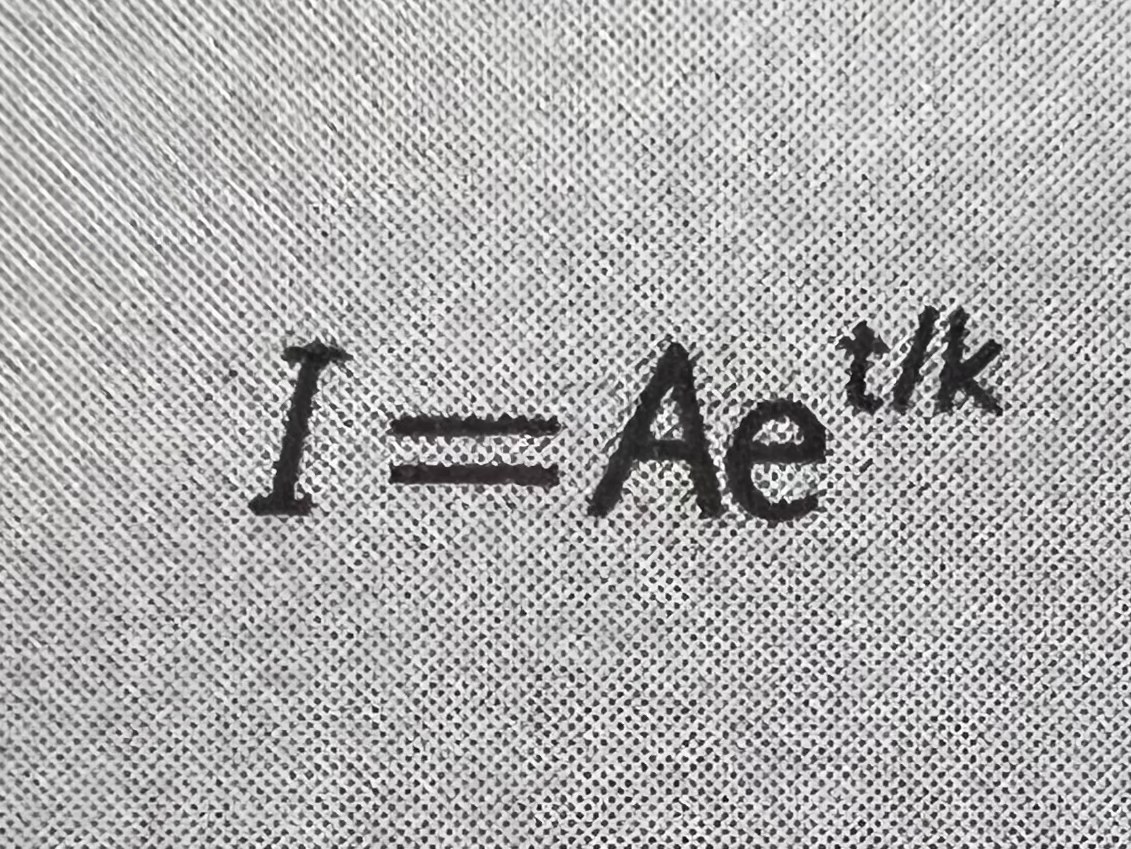
但是反抗度恒定是一个相当特殊的情况。由于前面章节提到一个或更多因素的作用，反抗度很可能会围绕人类基本水平下降，并且在跨界点和一定距离以外保持较低的水平（可能直到系统最终接近基本物理极限）。例如，假设在系统能够极大地促进自我设计并且导致每18个月能力便会倍增前，应用于系统的最优化力大致恒定（例如，O工 程 +O世 界 ≈C）。（这可能大致与摩尔定律下软件进步的速度曲线一致。）

如果是通过近乎不变的最优化力得到了速度提升，就会使反抗度下降成为系统力的倒数：

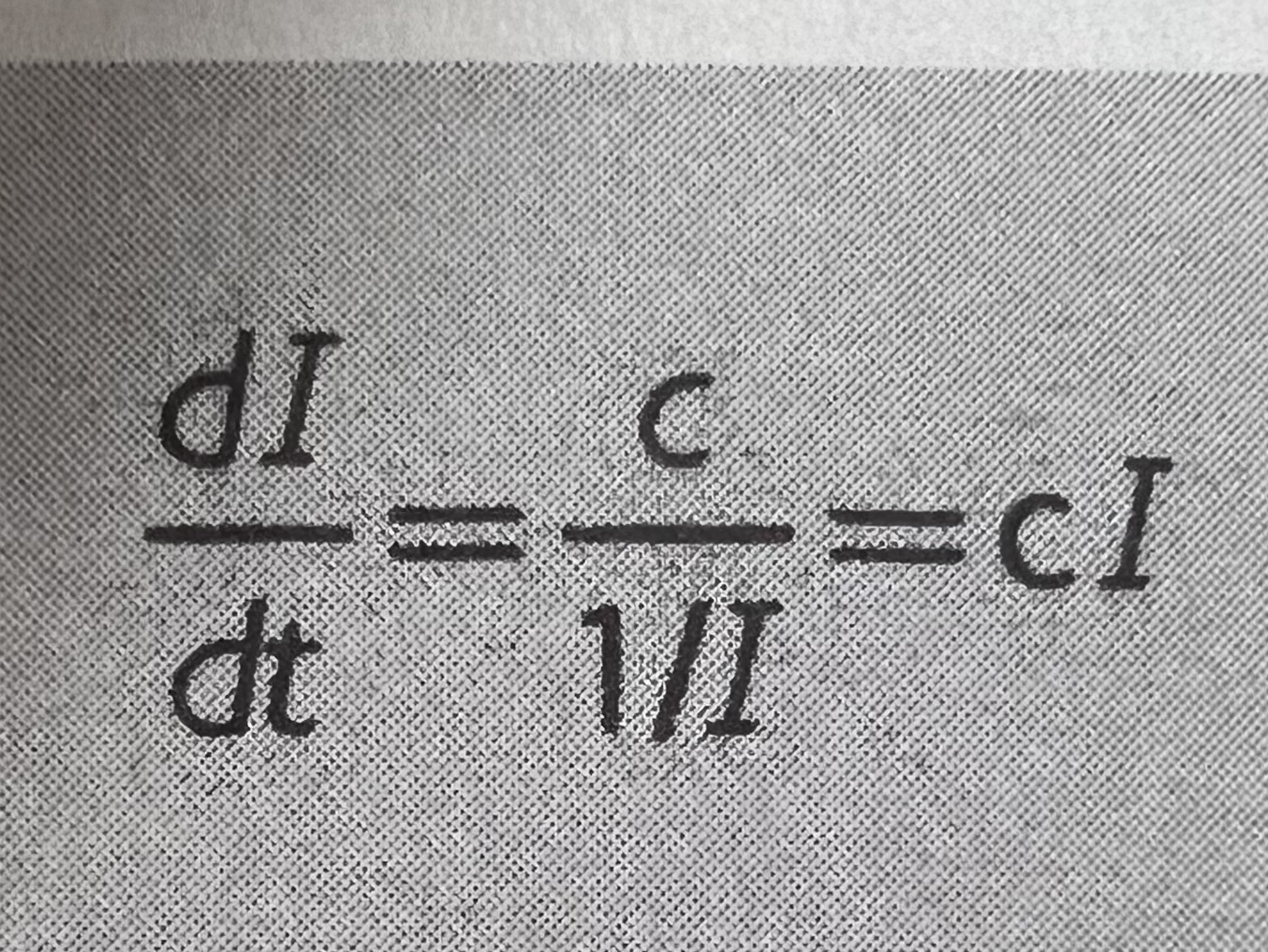
如果反抗度沿着双曲线模式持续下降，那么当人工智能到达跨界点时，应用于提高人工智能的全部最优化力就会翻倍，我们能够得出：

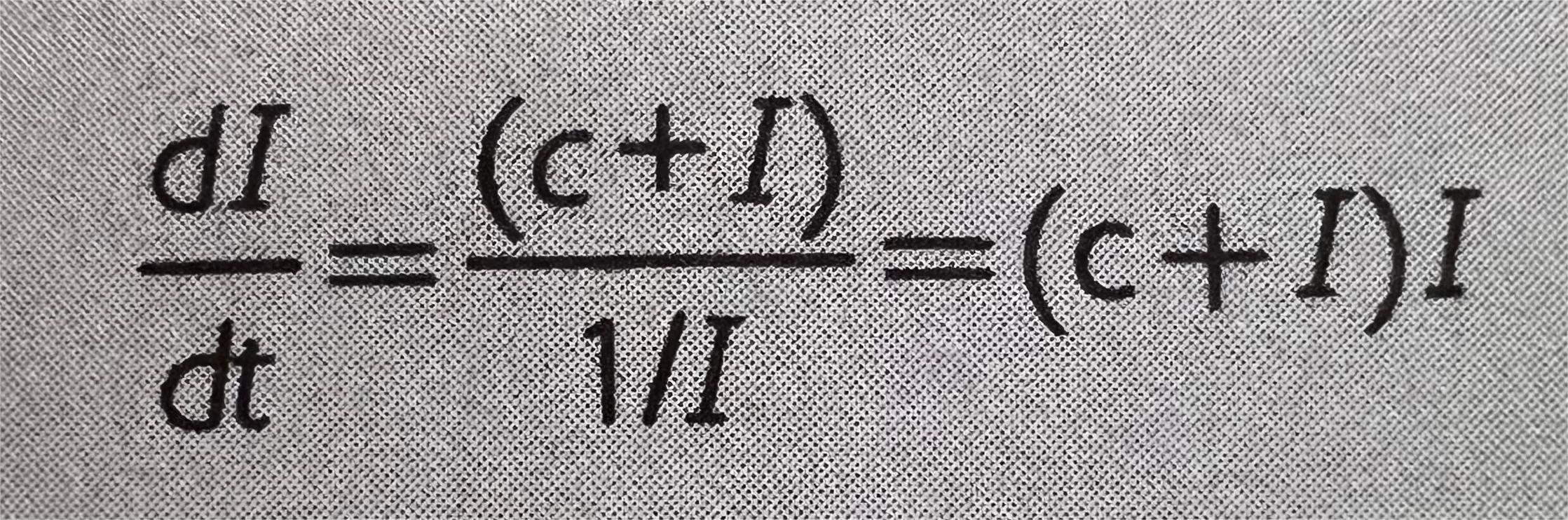
下一次倍增发生在7.5个月后。在17.9个月内，系统的能力增长了上千倍，于是便获得了速度超级智能（图4–3）。

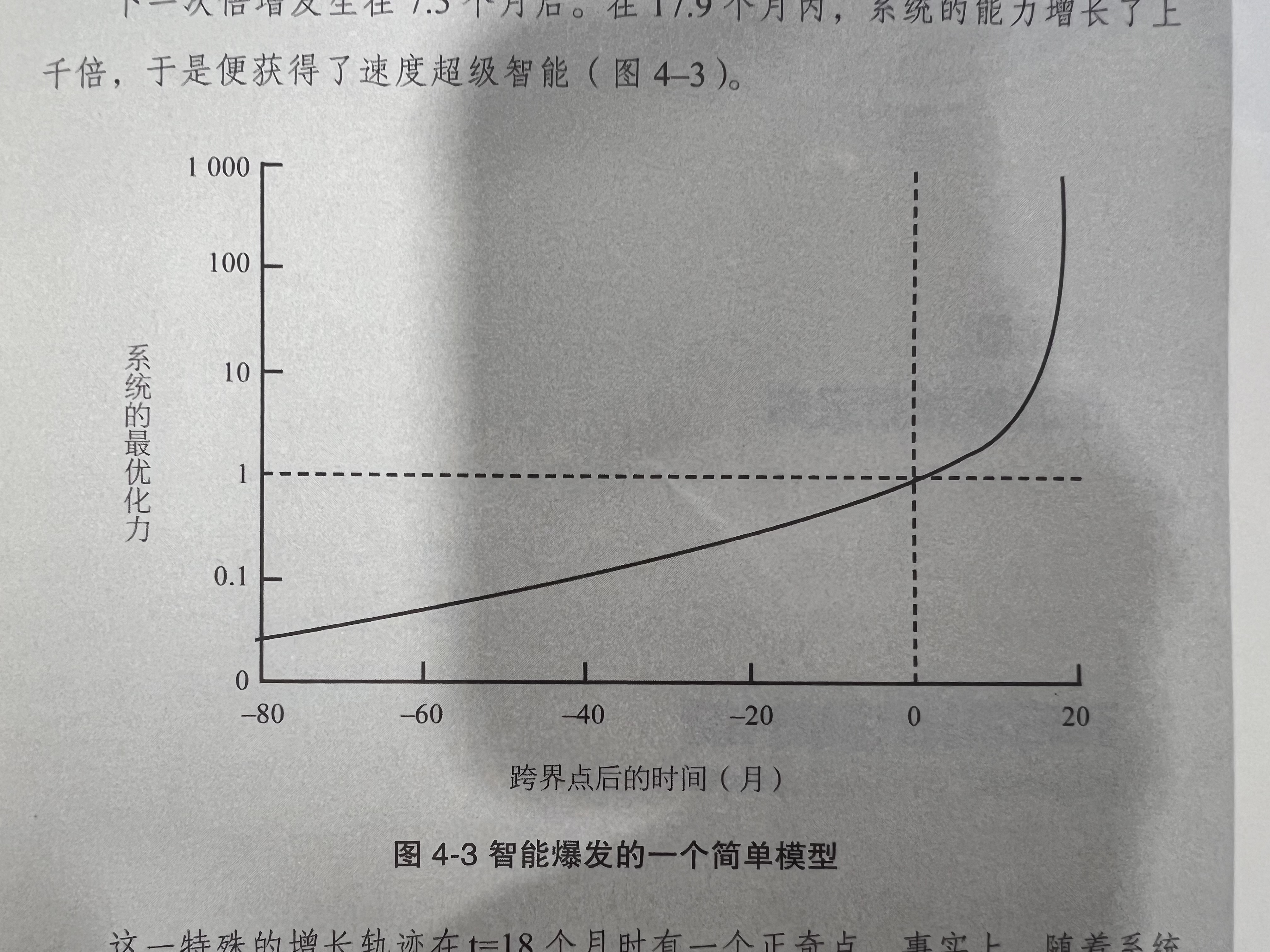
这一特殊的增长轨迹在t=18个月时有一个正奇点。事实上，随着系统开始接近信息处理的物理极限，反抗度保持不变的假设将不再成立。

这两种情况只是用于解释说明，也可能会出现许多其他轨迹，它们取决于反抗度曲线的形状。我们很容易就可以断言设置在跨界点周围的强反馈循环会强烈地趋向于使爆发比其本来可能的情况更快。